050 < >

Looks Like it Sounds--
or, those bizarre squiggles we call music. (part three)

Why do we write music the way we do and is it actually the best method? Dare we ask?
 

part one
part two

Western music has always had a certain bias toward pitches--we spend more time worrying about playing the right notes than we do about playing the right rhythms, and we don't spend nearly as much time on the subject in music class. When one 20th century composer was attempting to create a new way of arranging notes in musical compositions, someone asked him if he was going to systematize rhythm the same way and he replied, "we've never had a system of rhythm."

Actually, we have one, and it is even simpler than our system of pitches once was. And, like everything else about our written musical language, it got mad complicated (there's an expression I learned from generation Y).

When rhythm first came to be written down in the late Middle Ages, it came from a people who were blessed with a love of exactness. It seems hard to believe now, when a theory called Intelligent Design puts forth the idea that the bewildering complexity of the universe is a sign that it had to have come from the mind of a supreme being, but for a while people believed just the opposite--that the use of simple numbers, whole numbers, perfect 2 to 1 ratios, was what proved the existence of God. Well into the enlightenment, great thinkers continued to think that everything in nature pretty much fit together like a glove, and everything had its well ordered course. Even in ancient times (to us) philosophers talked of order and music as being one and the same. Naturally it was an order that could be easily grasped. Everything was in perfect harmony (society's great minds didn't see war up close back then, either). Even the planets were getting along glowingly. They called it the harmony of the spheres.

Notice it isn't the rhythm of the spheres. Rhythm has always had a bit of a problem being theologically and philosophically recognized.

Rhythm's part in all this, however, even if the church was too suspicious of it for a while to commit it to paper (remember, written music originated in the Christian church in the 9th century, see part one), is a series of simple 2 to 1 ratios. You may have learned in music class that a quarter note got one beat and a half note two and so on. That only holds up in certain situations (what exactly is a "beat," anyway?). What music teachers do not generally teach their young charges (and many do not grasp themselves) is that rhythmic notation is based today entirely on a series of ratios. Each note type in the pyramid below is related to the one in the succeeding line by being double in "size." Therefore it will take two notes of the next variety to equal the same amount of time taken by the one in the line above it. There are no fast notes or slow notes--they are only faster or slower than others--by a factor of exactly 2--, and depend entirely on their context. Such is the rhythmic system as we understand it today.

There is one small difficulty here, and that is that while two is a very simple and nicely reducible number, it isn't nearly as theologically justifiable as three, which is the number of the Trinity (and the magic number in a whole bunch of legends as well). Composers of the time were anxious to justify what they were doing, just as they are now, and the church wanted to make sure that they were writing good sound doctrine first, and aesthetically pleasing music would naturally have to follow. After all, how could the two be at odds?

This, too, is a simple matter. Given the same note pyramid, I can make every note nicely divisible into threes by putting dots after every note. In the Middle Ages, this was a much more popular option for composers in the church. Still, everything is either divisible into 2, or 3. A working knowledge of differential calculus is not required.

We are a long way from the rhythmic complexity of the 20th century. And just as the notion of notes being fixed on their lines and spaces becomes challenged when we introduce clefs (thus allowing what appears to be the lowest three notes in the illustration below to actually be higher than the notes that surround them)...

...once we introduce the concept of tempo, or the speed of a particular piece, there is no longer any guarantee that a quarter note in one composition or one part of a composition is necessarily going to be twice the speed of a half note in a different context. If they are together in the same part of the composition and the composer has not modified the speed of the piece with an instruction to speed up, or if I have not, because of my fancy or my historically grounded interpretation, given a little more or a little less time to one note and taken away some time from another (a concept called "rubato" which means "to rob") then a half note is held twice as long as a quarter note. But because this is a system of ratios, there is no definite amount of time involved. A quarter note could last a second, or half a second, or 3 seconds. It all has to do with the tempo. Thus, while a half-note will be twice as long as a quarter in any given piece, if the tempo suddenly changes, a half-note from a different part of the piece may actually be shorter than a quarter note in another part of the piece.  The only thing we can be sure of is how the notes relate to each other. It is similar to the gravitational pull on Jupiter, should you travel there. While gravitational pull itself remains constant, your experience of it on different planets does not. One thing remains the same (in this case, note values as they relate to each other) and one does not (how fast or slow notes actually go.)

I've noticed that people are slow to catch on to this. We can't help thinking that 16ths notes are fast, that quarters are fairly slow. They may not be, although, curiously, in our distance past, this may have held true. During the Renaissance there was a thing called "tempo guisto" which held that a quarter note was a fixed duration. How that was regulated exactly would be hard to know, this doctrine's home being an age before digital watches, or metronomes. (14-16th centuries A.D.)

It did require several notes to be created, of many durations, but all of them (minus the dotted ones) stand in a two to one relationship with the next member of the series. This means there are no ninth notes or twenty-seventh notes. You can't make a beat or a measure consist of 13 notes. At least you couldn't back then. And I'm not aware that anyone was heretical enough to find this annoying.

Composers eventually became dissatisfied with this, of course. This first thing to disrupt the unchanging speed of the notes was the introduction of the tempo mark. These were necessarily subject to the judgment of the individual, and they flourished in an era when "taste" was held in high regard. This was a sign of whether you had "taste": that you played works at appropriate tempi.

The markings are all borrowed from Italian, because it was another characteristic of that age that many musicians from Italy went to all parts of Europe and many parts of Europe thought the Italians were the best music makers. Most early operas bear this imprint: they are sung in Italian, and most of the musical terms they employ are also Italian. In Bach's time (early 1700s) tempo markings were not common. By Mozart's time everybody was using them. They were still generic--allegro for fast, adagio for slow, with occasional modifiers, like allegro ma non troppo (fast but not too fast) or allegro con brio (fast with life). These Italian terms had a stranglehold on European music, and even though Mozart (1756-1791) wrote an opera in German (taking advantage of a budding nationalist reaction against this foreign influence) it never occurred to him, as it did later with Beethoven (1770-1827) to actually use his native German language for instructions regarding tempo and expression.

The upshot of this "new" series of Italian tempo marks is that the musical example below on the left, though written in longer note values than the example on the right, may actually be a good bit faster. If the first piece were marked "Allegro" and the second "Adagio" it is likely that they would sound about the same. Even this is not easy to tell, however, since terms like fast and slow are in themselves only rough approximations and leave the exact speed up to the performer.  Mozart liked to complain about people taking his music too fast.

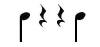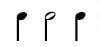
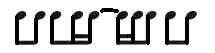
When a device called the metronome appeared, calibrated so that it would provide a given number of pulses per minute (60 is exactly one per second) it became possible for composers to specify exactly how fast they wished their compositions to be taken--if they were so inclined. And there does seem to have been a general desire on the part of composers for more and more control over each musical element as the twentieth century rolled by.

So much so, that, as we've just seen, what was once a pretty inflexible language in its graphic simplicity can either be adapted by modifying the graphic images themselves, or, in this case, bypassing them altogether by including instructions in another language--that is, English, or Italian, or German. By the middle of the last century some composers were bedecking their compositions with so much verbage it seemed the notes themselves were of secondary importance.

But composers in search of more flexible ways to notate the complex rhythms that can come into their heads have other methods. It became customary in the 19th century to indicate any stray number of notes that are supposed to fit within a beat (or several beats) by placing that unusual number above or below the notes. Those notes are beamed together and bracketed, to assure the performer that this is no misprint but an intentional flaunting of old convention. It is hard to know how Chopin (1810-49) would have survived without being able to do this.

Instead of the limited choices of 2, 4, 8, or 16 divisions of a beat, all the numbers in between are now available. Groups of 5, or 12, or even 17 notes per beat, or per measure, are permitted with this notational device.

Still, all of the notes above appear as though they must be evenly played. After all, they are still all of the same note value
1/22 of a measure!). Chopin would certainly not have played them this way. He would have given himself quite a bit of freedom from rhythmic exactness, and would have expected others to play his music that way.

The problem with this, of course, is that it opens up the whole question of things which are not written down, even in the musical scores themselves. Perhaps rhythm is still the most elusive musical element for this reason. It is one thing if a composer had no way to write down the way he actually played something. But even once notation had evolved so much complexity that there was no reason something couldn't be written down in very close approximation to the way in which is was played, composers continued to just assume people who played their works would know what they were doing.

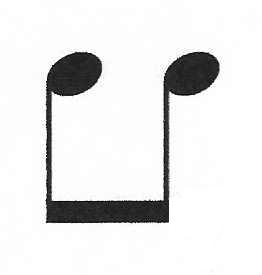
Above is a string of apparently even eighth notes. But if you were playing the blues, for example, you would most likely not play them evenly at all. You would "swing" them, meaning that the first of each pair would be about twice as long as the second, meaning they existed in more of a 2 to 1 ratio to one another. This could be easily notated

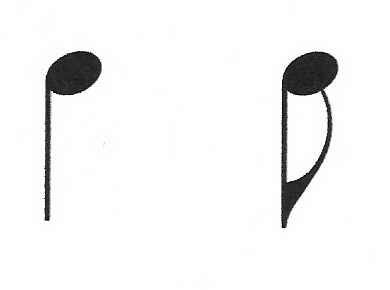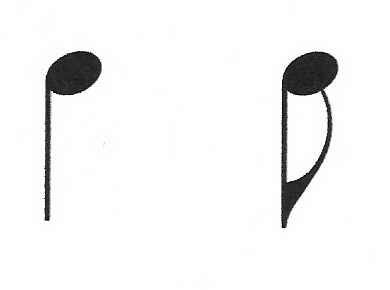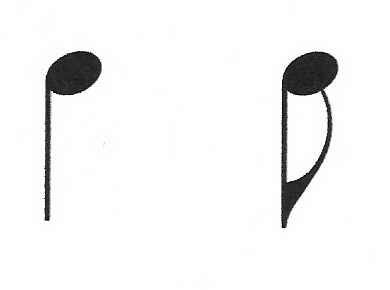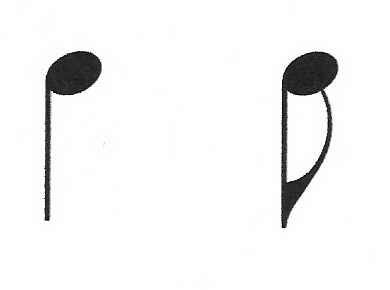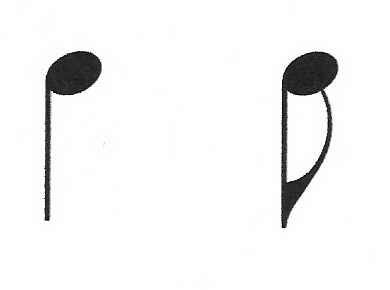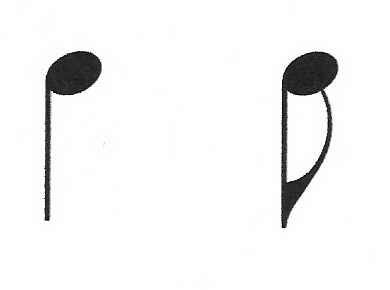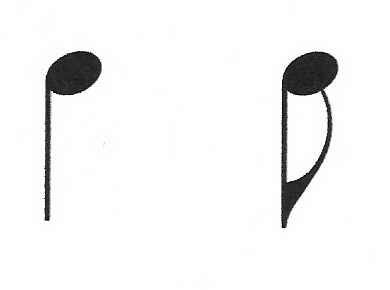
but it isn't. You are just supposed to know that based on the style of the music, these eighth notes are not to be played evenly. This is not exactly a new thing, however. Even before Bach's time there was a thing called "notes inegales" (unequal notes) which proceeding along a similar principle.

It is also customary, when playing a concert in a large hall, to sometimes pause slightly between musical ideas to let the reverberation die away so that the musical sense is clear. This is obviously not notated either, since music does not rely on one single location for its performance, and thus adjustments are always necessary owing to the venue (one interesting exception being the "Miserere" of Allegri which once upon a time by church fiat could not be performed anywhere else but St. Peter's).

But for those still irked by the apparent evenness of notes as they march across the page, allowing only that they be doubled or halved, a gradual speed up could be achieved by the following method, which flourished in the late twentieth century. It suggests that the eighth notes are gradually to become 16ths, and eventually, 32nds.

 It is less laborious than the method below, but a bit less exact:

The question, as always, is how much specific control the composer wishes to exercise over the music, and, of course, how complex his ideas are in the first place.

comments powered by Disqus